|
Electrónica Completa
Curso en
línea gratis de Electrónica Completa por el Ing. Alberto
Picerno
INTRODUCCIÓN del Capitulo
3
No queremos que
nuestros alumnos piensen a esta altura del curso que el
mismo es esencialmente teórico, y que todos los temas se
van a desarrollar en forma matemática. Pero tampoco
deseamos engañarlos indicándoles que no vamos a emplear
las matemáticas y la física. Desde ya le sugerimos que
si tiene presente estos temas los repase si quiere
aprender electrónica de un modo ordenado y entretenido
hurgando en las bases de las matemáticas y la física. No
le vamos a pedir más que lo que se estudia en el ciclo
básico de 8 años de cualquier país del mundo.
Inclusive pensamos incursionar en esos temas con ayudas
de videos de youtube que se generaran a medida que
avancemos con la electrónica. Sabemos inclusive que
muchos alumnos que pasaron hace mucho la edad escolar,
les gustaría tener un segundo trabajo, pero no se animan
a comenzar un curso de electrónica porque creen que se
requieren grandes conocimientos de matemática o física.
En el capítulo 1 Ud. tiene una muestra cabal de nuestros
requerimientos mínimos en esas ciencias. En realidad,
solo requerimos que sepa utilizar las operaciones
fundamentales de las matemáticas, suma, resta,
multiplicación, división, elevación al cuadrado y
algebra (aritmética de los símbolos). Inclusive no nos
interesa que puedan realizar esas operaciones a mano. Es
suficiente que sepan utilizar una calculadora científica
o la que viene incluida en el teléfono celular. Y si hay
alguna operación que no lograr entender, es
perfectamente válido que utilice la IA del WhatsApp. No
queremos loros que aprendan de memoria. Necesitamos
alumnos que sepan deducir conceptos. Que naveguen por
Internet averiguando temas que nosotros tratamos a
nuestro modo pero que otros autores pueden explicar de
otras formas.
Y como demostramos en el capítulo 2 vamos a hacer un uso
amplio de los laboratorios virtuales que ahora están a
su alcance económico. Inclusive vamos a utilizar dos: el
LW y el Multisim que utilizaremos más adelante.
Capitulo
3: Leyes de Kirchhoff
Las leyes (o
Lemas) de Kirchhoff fueron formuladas por Gustav
Kirchhoff en 1845, mientras aún era estudiante. Son muy
utilizadas en ingeniería eléctrica para obtener los
valores de la corriente y el potencial en cada punto de
un circuito eléctrico. Surgen de la aplicación de la ley
de conservación de la energía.
(La energía no puede desaparecer o crearse de la nada,
solo se puede obtener 1 energía a partir de otra).
Estas leyes nos permiten resolver los circuitos
utilizando el conjunto de ecuaciones al que ellos
responden. En la lección anterior Ud. conoció el
laboratorio virtual LW. El funcionamiento de este y de
todos los laboratorios virtuales conocidos se basa en la
resolución automática del sistema de ecuaciones que
genera un circuito eléctrico. Como trabajo principal la
PC presenta una pantalla que semeja un laboratorio de
electrónica pero como trabajo de fondo en realidad esta
resolviendo las ecuaciones matemáticas del circuito. Lo
interesante es que lo puede resolver a tal velocidad que
puede representar los resultados en la pantalla con una
velocidad similar aunque no igual a la real y de ese
modo obtener gráficos que simulan el funcionamiento de
un osciloscopio, que es un instrumento destinado a
observar tensiones que cambian rápidamente a medida que
transcurre el tiempo.
En esta entrega vamos a explicar la teoría en forma
clásica y al mismo tiempo vamos a indicar como realizar
la verificación de esa teoría en el laboratorio virtual
LW.
La
primera Ley de Kirchoff
En un circuito
eléctrico, es común que se generen nodos de corriente.
Un nodo es el punto del circuito donde se unen mas de un
terminal de un componente eléctrico. Si lo desea
pronuncie “nodo” y piense en “nudo” porque esa es
precisamente la realidad: dos o mas componentes se unen
anudados entre sí (en realidad soldados entre sí). En la
figura 1 se puede observar el mas básico de los
circuitos de CC (corriente continua) que contiene dos
nodos.
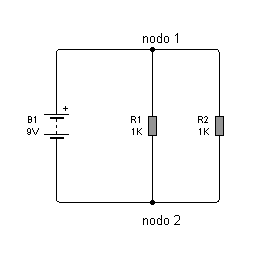
Fig.3.1 Circuito
básico con dos nodos
Observe que se
trata de dos resistores de 1Kohms (R1 y R2) conectados
sobre una misma batería B1. La batería B1 conserva su
tensión fija a pesar de la carga impuesta por los dos
resistores; esto significa cada resistor tiene aplicada
una tensión de 9V sobre él. La ley de Ohms indica que
cuando a un resistor de 1 Kohms se le aplica una tensión
de 9V por el circula una corriente de 9 mA
I = V/R =
9/1.000 = 0,009 A = 9 mA
Por lo tanto
podemos asegurar que cada resistor va a tomar una
corriente de 9mA de la batería o que entre ambos van a
tomar 18 mA. También podríamos decir que
desde la batería sale un conductor por el que circulan
18 mA que al llegar al nodo 1 se bifurca en una
corriente de 9 mA que circula por cada resistor, de modo
que en el nodo 2 se vuelven a unir para retornar a la
batería con un valor de 18 mA.
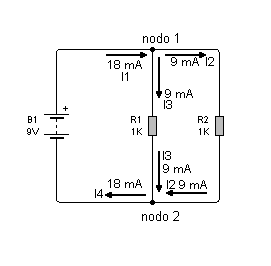
Fig.3.2 Aplicación
de la primera ley de Kirchoff
Es decir que en el
nodo 1 podemos decir que
I1 = I2
+ I3
y reemplazando
valores: que
18 mA =
9 mA + 9 mA
y que en el nodo
2
I4 = I2 +
I3
Es obvio que las
corriente I1 e I4 son iguales porque lo que egresa de la
batería debe ser igual a lo que ingresa.
Simulación de la primera Ley de Kirchoff
Inicie el LW.
Dibuje el circuito de la figura 3.2. Luego pulse la tecla
F9 de su PC para iniciar la simulación. Como no se
utilizó ningún instrumento virtual no vamos a observar
resultados sobre la pantalla. Pero si Ud. pulsa sobre la
solapa lateral marcada Current Flow observará un dibujo
animado con las corrientes circulando y bifurcándose en
cada nodo.
Para conocer el valor de la corriente que circula por
cada punto del circuito y la tensión con referencia al
terminal negativo de la batería, no necesita conectar
ningún instrumento de medida. Simplemente acerque la
flecha del mouse a los conductores de conexión y el LW
generará una ventanita en donde se indica V e I en ese
lugar del circuito. Verifique que los valores de
corriente obtenidos anteriormente son los correctos.
Para detener la simulación solo debe pulsar las teclas
Control y F9 de su PC al mismo tiempo.
Enunciado
de la primera Ley de Kirchoff
La corriente entrante a
un nodo es igual a la suma
de las corrientes salientes. Del mismo modo se puede
generalizar la primer ley de Kirchoff diciendo que
la suma de las corrientes entrantes a un nodo
son iguales a la suma de las corrientes salientes.
La razón por la
cual se cumple esta ley se entiende perfectamente en
forma intuitiva si uno considera que la corriente
eléctrica es debida a la circulación de electrones de un
punto a otro del circuito. Piense en una modificación de
nuestro circuito en donde los resistores tienen un valor
mucho mas grande que el indicado, de modo que circule
una corriente eléctrica muy pequeña, constituida por tan
solo 10 electrones que salen del terminal positivo de la
batería. Los electrones están guiados por el conductor
de cobre que los lleva hacia el nodo 1. Llegados a ese
punto los electrones se dan cuenta que la resistencia
eléctrica hacia ambos resistores es la misma y entonces
se dividen circulando 5 por un resistor y otros 5 por el
otro. Esto es totalmente lógico porque el nodo no puede
generar electrones ni retirarlos del circuito solo puede
distribuirlos y lo hace en función de la resistencia de
cada derivación. En nuestro caso las resistencias son
iguales y entonces envía la misma cantidad de electrones
para cada lado. Si las resistencias fueran diferentes,
podrían circular tal ves 1 electrón hacia una y nueve
hacia la otra de acuerdo a la aplicación de la ley de
Ohm.
Mas científicamente
podríamos decir, que siempre se debe cumplir una ley de
la física que dice que la energía no se crea ni se
consume, sino que siempre se transforma. La energía
eléctrica que entrega la batería se subdivide en el nodo
de modo que se transforma en iguales energías térmicas
entregadas al ambiente por cada uno de los resistores.
Si los resistores son iguales y están conectados a la
misma tensión, deben generar la misma cantidad de calor
y por lo tanto deben estar recorridos por la misma
corriente; que sumadas deben ser iguales a la corriente
entregada por la batería, para que se cumpla la ley de
conservación de la energía.
En una palabra, que la energía eléctrica entregada por
la batería es igual a la suma de las energías térmicas
disipadas por los resistores. El autor un poco en broma
suele decir en sus clases. Como dice el Martín Fierro,
todo Vatio que camina va a parar al resistor. Nota: el
Vatio es la unidad de potencia eléctrica y será
estudiado oportunamente.
Segunda
Ley de Kirchoff
Cuando un
circuito posee mas de una batería y varios resistores de
carga ya no resulta tan claro como se establecen la
corrientes por el mismo. En ese caso es de aplicación la
segunda ley de kirchoff, que nos permite resolver el
circuito con una gran claridad.
En un
circuito cerrado, la suma de las tensiones de batería
que se encuentran al recorrerlo siempre serán iguales
a la suma de las caídas de tensión existente sobre los
resistores.
En la figura
siguiente se puede observar un circuito con dos baterías
que nos permitirá resolver un ejemplo de aplicación.
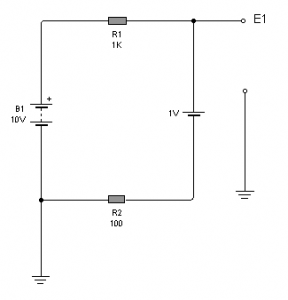
Fig.3.3. Circuito
de aplicación de la segunda ley de Kirchoff
Parece una ley
compleja de entender, pero la aplicación al circuito nos
va a ayudar enormemente. En la figura se puede observar
un circuito con dos baterías y dos resistores. Nosotros
deseamos saber, cual es la tensión de cada punto con
referencia al terminal negativo de B1 al que le
colocamos el símbolo de tierra que representa en forma
simbólica una conexión a nuestro planeta y al que
llamamos tierra o masa. Ud. debe considerar al planeta
tierra como un inmenso conductor de la electricidad.
Las tensiones de fuente, simplemente son las indicadas
en el circuito, pero si pretendemos aplicar las caídas
de potencial en los resistores, debemos determinar
primero cual es la corriente que circula por el resistor. Para
determinar la corriente, primero debemos determinar cual
es la tensión de todas nuestras fuentes sumadas. Observe
que las dos fuentes están conectadas de modos que sus
terminales positivos están conectados
entre si por el resistor R1. Esto significa que la
tensión total no es la suma de ambas fuentes sino la
resta. Con referencia a tierra, la batería B1 eleva el
potencial a 10V pero la batería B2 lo reduce hacia 1 V.
Entonces la fuente que hace circular corriente es en
total de 10 – 1 = 9V . Los electrones que circulan por
ejemplo saliendo de B1 y pasando por R1, luego pierde
valor en B2 al atravesar R2. Para calcular la
corriente circulante podemos agrupar entonces a los dos
resistores y a las dos fuentes tal como lo indica la
figura siguiente con el fin de aplicar la segunda ley.
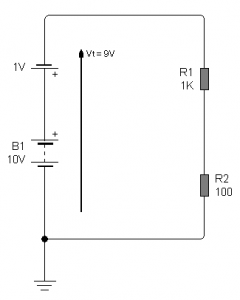
Fig.3.4
Reagrupamiento del circuito
¿El circuito de
la figura 3.4 es igual al circuito de la figura 3.3? Si,
este reagrupamiento solo se genera para calcular la
corriente del circuito original. De acuerdo a la ley de Ohms
I =
Et/R1+R2
Y esto es así porque los
electrones que salen de R1 deben pasar forzosamente por
R2 y entonces es como si existiera un resistor total
igual a la suma de los resistores
R1 + R2 = 1100 Ohms
Se dice que los
resistores están conectados en serie cuando están
conectados de este modo, de forma tal que ambos son
atravesados por la misma corriente igual a
I = (10 – 1) / 1000 +
100 = 0,00817 o 8,17 mA
Ahora que
sabemos cual es la corriente que atraviesa el circuito
podemos calcular la tensión sobre cada resistor. De la
expresión de la ley de Ohm
I = V/R
se puede
despejar que
V = R . I
y de este modo
reemplazando valores se puede obtener que la caída sobre
R2 es igual a
VR2 = R2 . I = 100 .
8,17 mA = 817 mV
y del mismo modo
VR1 = R1 . I = 1000 .
8,17 mA = 8,17 V
Estos valores
recién calculados de caídas de tensión pueden ubicarse
sobre el circuito original con el fin de calcular la
tensión deseada.
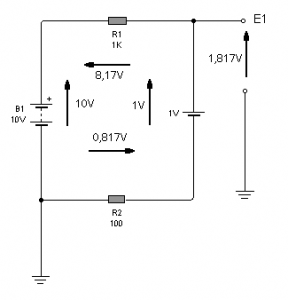
Fig.3.5 Circuito
resuelto
Observando las
cuatro flechas de las tensiones de fuente y de las
caídas de tensión, se puede verificar el cumplimiento de
la segunda ley de Kirchoff, ya que comenzando desde la
masa simbólica de referencia y girando en el sentido de
las agujas del reloj podemos decir que
10V –
8,17V – 1V – 0,817 = 0 V
o realizando una
transposición de términos y dejando las fuentes a la
derecha y las caídas de tensión a la izquierda podemos
decir que la suma de las tensiones de fuente
10V –
1V = 8,17V + 0,817 = 8,987 = 9V
Y además podemos
calcular fácilmente que la tensión sobre la salida del
circuito es de
0,817V
+ 1V = 1,817V
Con respecto a
tierra o al negativo de B1, con la polaridad
indicada en el circuito es decir positiva.
Trabajo
práctico en el laboratorio virtual
Nuestro trabajo
práctico consiste en dibujar el circuito en el LW.
Activarlo con F9 y recorrerlo con el cursor anotando las
caídas de tensión y la corriente en cada punto del
mismo. Se podrá verificar el cumplimiento estricto de
los valores calculados.
Posteriormente lo invitamos a resolver otro circuito que
es el indicado a continuación para el cual le damos una
ayuda.
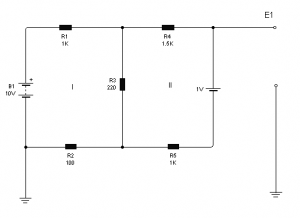
Fig.3.6 Circuito
para resolver por el alumno
La ayuda que le
vamos a dar es la siguiente:
1) Considere al circuito completo como construido con
dos mayas. La maya I y la maya II. Resuelva la corriente
en la malla I solamente, suponiendo que la II esta
abierta.
2) Luego haga lo
propio con la malla II; cada malla va a generar una
corriente por R3.
3) Súmelas
considerando sus sentidos de circulación y obtendrá la
corriente real que la recorre cuando las dos mallas
están conectadas y de allí podrá calcular la caída de
tensión sobre R3.
4) Luego debe
obtener las otras caídas de tensión y establecer la
segunda ley de Kirchoff.
5) Por último
calculará la tensión de salida V1.
6) Luego dibuje
el circuito en el LW y verifique que el resultado
hallado corresponda con el circuito virtual y por
supuesto con la realidad.
Descarga Leccion 3
de LIVEWIRE <<Clic Aqui>>
Descarga Trabajo
Practico 3 de LIVEWIRE <<Clic Aqui>>
Conclusiones
De este modo ya estamos en poder de valiosas
herramientas de trabajo que se utilizan todos los días
en la resolución de circuitos electrónicos simples, que
ayudan al reparador a determinar los valores de tensión
y corriente, existentes en los circuitos.
En la próxima lección, vamos a trabajar con fuentes de
tensión alterna aplicadas a circuitos con resistores.
Posteriormente, vamos a presentarle los dos componentes
pasivos que acompañan al resistor en los circuitos mas
comunes: el capacitor y el inductor y en poder de todo
este conocimiento, le vamos a explicar como armar y
probar su primer dispositivo útil; una radio elemental
que nos permitirá conocer conceptos muy importantes de
la electrónica.
|
